Shay's Maths and Art

Tag: Algebra

  • Abstract Nonsense

    “Why is a raven like a writing desk?”

    The mad hatter hadn’t the slightest idea and Lewis intended it to remain unanswered, but the question does suggest that ravens and writing desks are similar. How would they be similar or even the same? In mathematics, this question is taken very seriously, not necessarily for fictional riddles by fictional characters but for fictional riddles by real people.

    An example a question like this is,

    “When are two sets the same?”

    To be clear, a set just is a collection of things nothing more. The things could be anything, they could be all things in the observable universe, the counting numbers, the teams in the grand final but note that to describe what was in the set, we had to refer to the context of the things or what the things do.

    But when are two sets the same? We could say they are the same when they contain the same things but then we would need to understand what sameness means for the things. As an example, consider the two sets \{ a,\,b,\,c \} and \{ 1,\,2,\,3 \}. One look and we can see they are sets of different things and so must be different sets, but they are similar. For instance they both contain three things and if we ignore the shape of the symbols and the meaning we put onto them, then we just have two sets of three things. Thinking of these two sets only as sets lets us see how similar can be.

    The way mathematicians like to show two sets are the same is to show that each thing in one of the sets has a partner in the other. This would be called a one-to-one correspondence and is a kind of way sets relate to one another.

    There are many ways two sets of different sizes can be related but one-to-one correspondences allow us to have a notion of sameness in the category of sets.

    But what about the category of all universes or the category of grand finals? How do we talk about sameness here?

    Introducing Category Theory. This the theory of mathematical categories and is way of looking at sameness in a different way. But first,

    What is a category?

    Categories are more about movement and how things relate whereas sets are static things in themselves. The definition of a category is as follows:

    A category is a collection of objects,

    and arrows between objects,

    We can imagine the objects A and B to be places and the arrow f to be a movement from A to B. Just like catching a train and moving from station to station, moving from A to B and then from B to another place C is as if we went from A to C in one swift movement.

    g\circ f is the composition of f with g

    We can also make round trips there and back again, as if we didn’t leave at all.

    Here \text{id}_A is called the identity arrow

    These identity arrows are important to our categorical idea of sameness explained later but the meaning of such non-movements is that moving from one object to another and then take staying in place is equal to just the first movement. The final rule is that we can take any path like in the diagram below

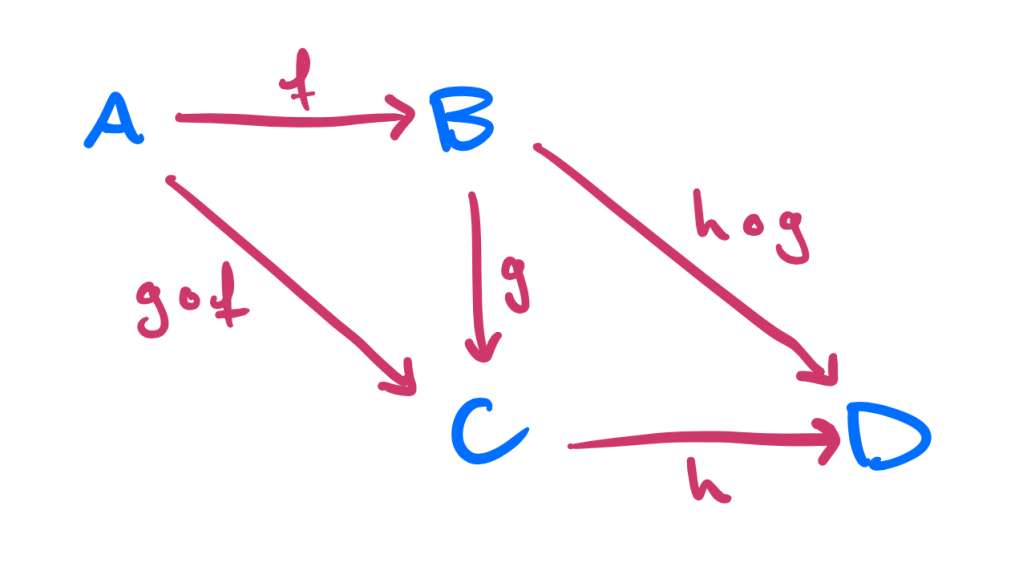
    h\circ (g\circ f) = (h\circ g)\circ f i.e. brackets don’t matter!

    One of the main points of category theory is that we can talk about properties of objects without referring to what the objects are directly. Now if I want to say two objects A and B are the same then I need to make sure there is a path f to move from A to B and back again along the path g without changing anything. I also need to make sure the same is true when starting at B then moving to A and back again.

    g\circ f = \text{id}_A and f\circ g=\text{id}_b

    The idea is that these movements between objects carry along with them only the properties we care about. The technical term for such a movement f is isomorphism, where iso– means “the same” and –morphism is the just morphing from one object into another. Isomorphisms capture the essence of the sameness between two things by identifying what aspects of the two things we mean to be the same because if absolutely everything between the two things were the same, could we even say we have two things?

    So why is a raven like a writing desk? We have a slight idea, though the answer will depend on which category containing collections of ravens and writing desks you’re referring to.

    References:

    Baez, John C., and James Dolan. “Categorification.” In Higher Category Theory, eds. Ezra Getzler and Mikhail Kapranov, Contemp. Math. 230, American Mathematical Society, Providence, Rhode Island, 1998, pp. 1-36.

    https://doi.org/10.48550/arXiv.math/9802029

    Carroll, Lewis.Alice’s adventures in Wonderland .[New York, Boston, T. Y.Crowell & co, 1893]

    Illustration by Shay Tobin

    , ,